IQR Calculator

What Is IQR ?

IQR is a measure of statistical dispersion, being equal to the difference between the third and first quartiles. IQR Calculator is used to calculate the interquartile range of a set of numbers.Quartile means 25th of the data.

How to calculate Interquartile Range ?

The Interquartile Range (IQR) is a measure of variability, based on dividing a dataset into quartiles.

Here's how you can calculate the IQR:

• Order the data set from smallest to largest.
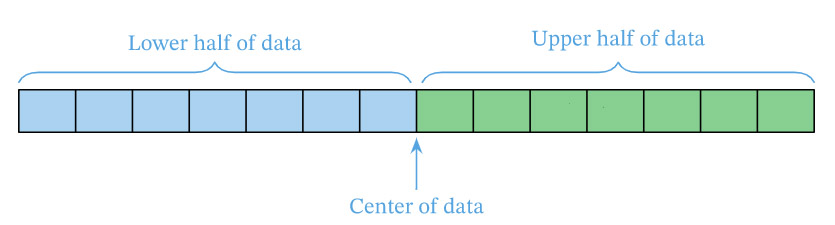
• Calculate the first quartile (Q1), which is the median (middle value) of the lower half of the data set.
• Calculate the third quartile (Q3), which is the median (middle value) of the upper half of the data set.
• The Interquartile Range is then calculated by subtracting Q1 from Q3: IQR = Q3 - Q1

The Interquartile Range is defined as the difference between the first quartile (Q1) and third quartile (Q3).

Formula :

The formula for Interquartile Range (IQR) is:

IQR = Q3 - Q1

where Q1 is the first quartile (25th percentile) and Q3 is the third quartile (75th percentile).

The following is the interquartile range calculation formula:

Calculation Of Q1 In Dataset ?

In statistics, the first quartile (Q1) is a measure of central tendency that represents the value separating the lowest 25% of a dataset from the upper 75%. In the context of calculating the interquartile range (IQR), Q1 is the median of the lower half of the dataset.

To calculate Q1, you need to follow these steps:

1. Sort the dataset: Arrange the dataset in order from lowest to highest.
2. Find the median: Determine the median value of the dataset. If the dataset has an odd number of values, the median is the middle value. If the dataset has an even number of values, the median is the average of the two middle values.
3. Divide the dataset: Split the dataset into two halves. If the median value is included in the dataset, include it in both halves.
4. Find the median of the lower half: Calculate the median of the lower half of the dataset. This is Q1.

For example, let's say you have the following dataset:

{10, 15, 20, 25, 30, 35, 40, 45, 50, 55}

Sort the dataset: {10, 15, 20, 25, 30, 35, 40, 45, 50, 55}

Find the median: The median is 30.

Divide the dataset: Split the dataset into two halves: {10, 15, 20, 25, 30} and {35, 40, 45, 50, 55}.

Find the median of the lower half: The median of the lower half is 20. This is Q1.

In this example, Q1 is 20, which means that 25% of the data falls below 20 and 75% of the data falls above it.

Once you have found Q1, you can then calculate the third quartile (Q3) and the interquartile range (IQR) to provide information about the spread of the dataset.

Calculation Of Q3 In Dataset ?

In statistics, the third quartile (Q3) is a measure of central tendency that represents the value separating the upper 25% of a dataset from the lower 75%. In the context of calculating the interquartile range (IQR), Q3 is the median of the upper half of the dataset.

To calculate Q3, you need to follow these steps:

1. Sort the dataset: Arrange the dataset in order from lowest to highest.
2. Find the median: Determine the median value of the dataset. If the dataset has an odd number of values, the median is the middle value. If the dataset has an even number of values, the median is the average of the two middle values.
3. Divide the dataset: Split the dataset into two halves. If the median value is included in the dataset, include it in both halves.
4. Find the median of the upper half: Calculate the median of the upper half of the dataset. This is Q3.

For example, let's say you have the following dataset:

{10, 15, 20, 25, 30, 35, 40, 45, 50, 55}

Sort the dataset: {10, 15, 20, 25, 30, 35, 40, 45, 50, 55}

Find the median: The median is 30.

Divide the dataset: Split the dataset into two halves: {10, 15, 20, 25, 30} and {35, 40, 45, 50, 55}.

Find the median of the upper half: The median of the upper half is 45. This is Q3.

In this example, Q3 is 45, which means that 25% of the data falls above 45 and 75% of the data falls below it.

Once you have found Q1 and Q3, you can then calculate the interquartile range (IQR) by subtracting Q1 from Q3. The IQR is a measure of variability that indicates the spread of the middle 50% of the dataset.

Where To Use IQR Calculation ?

The Interquartile Range (IQR) is commonly used in descriptive statistics to summarize the spread of a dataset. Some of the applications of IQR in statistics include:

1. Outlier detection: IQR can be used to identify outliers in a dataset. An outlier is a value that lies outside the range of 1.5 times the IQR below the first quartile (Q1) or above the third quartile (Q3).
2. Data normalization: IQR can be used to normalize data by transforming it into a standard scale. This is often used in machine learning and data analysis.
3. Box Plot visualization: IQR is used to construct box plots, which are a visual representation of a dataset's spread and skewness.
4. Robust measures of dispersion: IQR is a robust measure of dispersion, meaning it is less affected by outliers and extreme values than other measures such as range or standard deviation.
5. Comparison of datasets: IQR can be used to compare the spread of two or more datasets to see if they are similar or different.